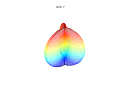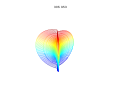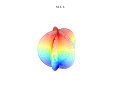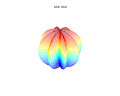知识库
Browse the glossary using this index
Special | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | ALL
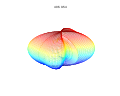
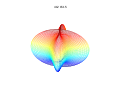
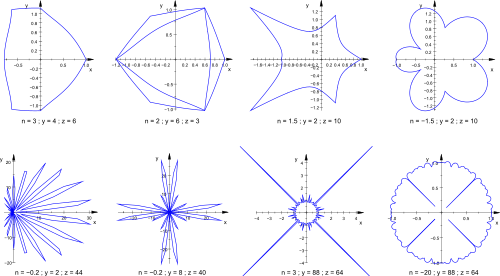
Superformula超级方程式 📖算法说明 ▶️曲线绘制过程演示 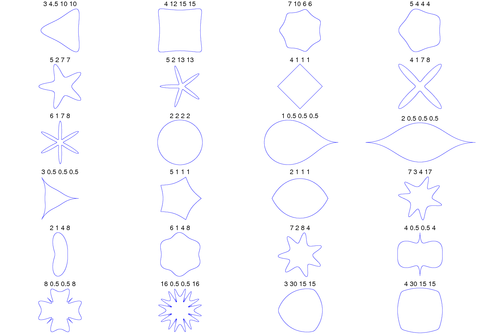 超级公式是超椭圆的推广,由 Johan Gielis 在 2000 年左右提出。 Gielis 认为该公式可以用来描述自然界中存在的许多复杂形状和曲线。Gielis 已提交与超级公式生成的模式合成相关的专利申请,该专利于 2020 年 5 月 10 日到期。 在极坐标中,有 通过为参数选择不同的值 该公式是对超椭圆进行推广得到的,由丹麦数学家皮特·海因命名并推广。 在以下示例中,每个图上方显示的值应为m、n 1、n 2和n 3。 通过超级公式的球积,可以将公式扩展到 3、4 或n维。例如,通过将两个超级公式r 1和r 2相乘获得3D参数化表面。坐标由以下关系定义:
3D超级公式:a = b = 1;m、n 1、n 2和n 3显示在图片中。 可以通过在超级公式的两项中允许不同的m个参数来概括超级公式。通过替换第一个参数{\displaystyle m} 这允许创建旋转不对称和嵌套结构。在下面的例子中 a, b、 | |